Barbenheimer Is the Bomb

Barbenheimer is a rare beast, an unintentional, organic marketing crossover, an absurd juxtaposition that promises loads of ironic, hi-tech, dystopian humor. It is all that, but it's so much more besides: a mix of opposites so combustible it’ll blow your mind if you let it.

I didn't even watch a trailer for Barbie, and I assumed it would be a fluffy, light-hearted farce. It’s not. It’s a nuclear-tipped cultural missile of wokeness launched by Hollywood directly at the beating red heartland of America. The film is directed by Greta Gerwig, one of Time’s 100 Most Influential People who I’d never heard of but will pay attention to from now on. Intensely self-conscious and self-deprecating, Barbie is filled with sincere yet hilarious feminist rage, stylistic home runs every second of runtime, and flagrant male homoeroticism that’s pervasive, yet never directly acknowledged. No wonder conservatives hate it, with Ben Shapiro and others acting surprised and hurt that the PG-13 movie isn’t suitable for young children and doesn’t portray the values they think it should. This hand-wringing and backlash is the latest evidence yet that conservatives have neither self-awareness nor a sense of humor.

I knew I had misjudged the film early on, when Margot Robbie’s Stereotypical Barbie became Pervasive Thoughts of Death Barbie. The movie never lets up, naming every bad thing about living as a woman--or a person, really--in our patriarchal, capitalistic society. In the process, Ryan Gosling's Ken goes on his own journey of self-discovery, transforming from an empty-headed muscle man into a 3-dimensional human being. Humanity, decency, and emotional intelligence. That’s what the right are calling “toxic femininity”. If that’s what it takes to kill toxic masculinity, then let the duel of poisons begin.

Barbie is as serious as a heart attack, but aside from one ill-advised and overlong monologue near the end, the message is wrapped in a fun and funny package that is indeed very pink. Unless you’re a conservative snowflake who can’t take a joke, go see it.

I knew Oppenheimer’s story, at least at a high level. And with man’s man Christopher Nolan directing, it was exactly as ponderous, self-aggrandizing, and dramatic as I expected. Full of A-List male actors and man’s man Emily Blunt, the film tells the grand story of the man who led America’s project to build the (so far) most terrible weapon ever. In contrast to Barbie’s feminist world of girl stuff, malleable men, and honest humanity, Oppenheimer glorifies patriarchy’s holy trinity: power-hungry politicians, useful-idiot soldiers, and the scientists who have all the real power, but give it away for peanuts to the former two groups.

Nolan has the chutzpa to portray Oppenheimer as a tragic, misunderstood, and unfairly attacked hero, despite the movie ending with the revelation that he knew all along exactly what the politicians and generals would do with the bomb. Did they really have “no choice”, as they liked to believe? The war was essentially won without the bomb, and the Manhattan Project let the anti-labor Democrat Harry Truman start the Cold War and the nuclear arms race. The brutal hegemony of the United States has put a lot more than blood on Oppenheimer’s hands.

But the movie, released in our contemporary day, isn’t about the bomb. It’s about AI (I know, everything's about AI for me, but it's really true this time). This was clear to me the moment Cillian Murphy’s J. Robert Oppenheimer climbed the tower in Los Alamos, alone, to commune with the Trinity device. He regarded this slumbering mechanical lump of potential energy in all it’s alienness, yet still decided to give it life. They thought for a while that setting off an atomic bomb would ignite a nuclear chain reaction in the atmosphere, destroying all life on earth. At the time of the Trinity test, the odds of that happening were still non-zero, yet they went ahead anyway. The parallel to today’s AI researchers isn’t just analogous, it’s an exact repetition. Many AI researchers give it about a 10% chance of destroying humanity, yet they’re building it anyway, knowing it’ll be used by the most ruthless of capitalists and governments to bring on a new hegemony.

As the movie made clear, the politicians and generals needed the physicists. If the nerds of that day had actually had any brains and/or balls, and all refused to build bombs, maybe we could be living in a peaceful world with abundant nuclear energy. But they whored their power to the politicians, the most widely despised people on the planet. Likewise, today’s AI researchers could form their own non-profit, people-centered Manhattan Project to benefit all humanity. Instead, the AI arms race they’ve started means we’re likely to see a shooting war between the US and China, and the world's people will be enslaved to AI masters regardless of who wins. Not because AI is evil, but because the only people who can build it are giving it to the people least suited to wield it. Today’s AI scientists would do well to notice how the politicians not only discarded Oppenheimer when they no longer needed him, they tried to humiliate and destroy him when he dared speak about how to use the bomb he had helped create. But since Oppenheimer was smart enough to foresee this, he has only himself to blame.

The last interesting thing I’ll comment on is how Mattel not only allowed their IP to be used in the movie, they produced the film. I think it’s brilliant in the way only a for-profit company can be brilliant in a way that looks totally stupid. They created a movie that acknowledges and condemns all the harm their toy has done and continues to do, while portraying the corporation itself in the most unflattering possible light. While a scientist or engineer will only prostitute themselves if they look cool doing it, a corporation will happily shit on itself and its employees if it’ll make a buck, which of course it will. From Mattel's support of this film, I tentatively assert that corporations are easier to align to human needs than governments, though not by much.

So what is Barbenheimer? A contest of pink vs. dark aesthetics? If so, Barbie obliterates Oppenheimer, which looks so ugly in comparison. A contrast in silly vs. serious filmmaking? Not at all; both movies are weighty. Barbenheimer is a choice we need to make as a society. Do we want death-worshiping masculinity or life-affirming femininity to lead us forward?

Why Are Websites So Annoying?

 The UI design world has gone crazy.  A few arbitrary trends have become nearly ubiquitous despite being universally annoying.  Why is annoying your potential customers so popular?

1.  The most obvious feature of websites today is the inevitable popup that the designers shove in your face before you’ve even had a chance to view the rest of the site.  (Perhaps even worse is the variant where they give you 10 or 20 seconds to settle in and start digesting their content, only to interrupt you with the popup then).  Enjoying our site?  I just got here.  Give me a chance to form an opinion.  Like us!  Subscribe!  Get a discount!  Now or never!
   
   These popups are so infuriating I wish I could choose to simply never again visit any site that assaulted me in this way.  But if I did that, I’d need to give up using the web entirely.  The practice is nearly universal.  Why is there no innovation or differentiation in this area on different websites?  It would be a competitive advantage to offer a peaceful website that didn’t use popups.  There are plenty of other ways to offer discounts or solicit newsletter subscriptions.  I seriously doubt these popups are the most effective. 
   
   I know popup blockers exist, but they have drawbacks.  Sometimes they block functionality I want.  Sometimes websites detect popup blockers and refuse to work.  Plus, why should I need third-party protection?  Why don’t websites use techniques that actually make the sites appealing and easy to use?  The most successful websites in the world (think Google and Amazon) don’t use popups.
   
   Note that I’m not talking here about the “We use cookies” notices that every web site employs.  They have no choice about this because it’s legally required by Europe’s GDPR law.  This well-intentioned but ultimately annoying and useless provision has increased privacy and data control by exactly zero for the average user while degrading our web experience.
   
   

2. Hover everything.  So many websites do stuff when you hover over things on the screen.  Menus that expand on hover are the most prevalent, but often hovering over an item on a list is used as a sort of soft selection that causes additional information to be displayed.  Some video sites will even start playing the video if you hover over it for too long.  Perhaps most annoying is buttons that don’t show up unless you hover over the right area of the screen.  How were we supposed to know this option was available like this?  Do you expect us to hover over the entire screen to try to discover what commands are available?
   
   The main problem with hover everything is that it’s not safe to leave your cursor anywhere.  You have to actually spend time to find a safe place to rest your cursor so you can actually view the website without interference. 
   
   And since hovering isn’t even possible with a phone or tablet, why would anyone build in hovering as a major component of their site?
   
   

3. Flat design.  This disease affects the Windows operating system perhaps even more than it affects web sites.  In my opinion, Windows design peaked with Windows XP.  In those good old days, you could tell a button was a button because it had a 3-D appearance that looked like a physical button.  Old websites worked the same way. In this way, the computer was adapting itself to the way our minds work in our everyday world.  Nowadays, button-like UI widgets are distinguished from inactive elements by more subtle characteristics like fonts and layout.  The only way you can know for sure if a UI element is clickable is to hover over it and see if it changes in a way that says “click me”.  We are forced to learn the “design language” an OS or website uses in order to become effective with that interface. 
   
   Flat design not only makes interfaces difficult to learn, it can make them completely unusable.  Now that Windows title bars and borders are completely flat and colorless, it’s impossible to tell where one window ends and the next one begins.
   
   And since different UI elements are all flat and as colorless as possible, it’s not easy for websites to become beautiful and differentiated from each other.  Why is flat design so ubiquitous?  Why no innovation or differentiation?  

The “why” question about these UI design trends is pretty confusing.  My theory is that the designs are being driven from the technical side and decisions are being made based on what’s possible and easy to implement instead of from the design and marketing side driven by what would create a great user experience.

I think my theory is supported by the way “exit intent” popups appeared on the web all at once like a fit of collective hysteria.  These are the popups that appear when you quickly move your cursor towards the part of the screen where you can switch and close tabs.  Wait!  Don’t go!  Why don’t you like us?   Please like us!  We’ll do anything if you don’t leave!  You’ll be sorry if you leave now!  Please do free labor to tell us how to do our jobs better!

One day in 2012, somebody figured out how to determine exit intent and this mechanism spread like wildfire since it met an existing need in traditional marketing, namely customer retention.  They actually use phrases like “page abandonment” to describe user behavior.  Feel insecure much?

Does anyone actually respond to these desperate and disruptive UI features?  I expect very few do.  But it must be non-zero, or else nobody would use them, just like how spam and junk mail wouldn’t exist if zero people responded to them.  But is it really worth it to them to receive these few conversions at the cost of annoying everyone else?  I read a few sources that say popups do indeed work, but that they’re not worth the cost.  In addition to user annoyance, popups will lower your search engine rankings because Google penalizes the behavior.  So it’s possible that design decisions are being made at least partially from the marketing side, but by dumb marketers.

Unfortunately, I don’t think there’s much we can do about these annoyances.  We’ll simply have to wait until some large company or explosive startup creates a new trend.  How about “clean design” or “intuitive design”?  Websites can do something called A/B testing, where they have two different site designs that are presented randomly to half of their customers.  They can then measure which design performs better and then roll that out to everyone.  Someday--soon, I hope--a major A/B testing result will show that these design trends provide an overall decrease in website performance.  Amazon has proved that great user experience sells, so eventually others should come to their senses.

How To Solve Wordle More Often and Possibly Ruin the Game

 

If you’re reading this, then you probably play Wordle or are at least curious about it.  There are many appealing features of the game, including the social aspect and the fact that it’s limited to one play a day.  If you particularly enjoy these features, then my advice on how to get better at the game may not be desirable.  But if you just want to get better at solving the puzzles more of the time, read on.

The first way to get better is to play more often.  Of the many Wordle clones and variants available, I’ve found https://octokatherine.github.io/word-master/ to be the best for just practicing.  It has the exact same rules as Wordle, but the tiles turn faster and you can play as many times as you want.  Just using this site will make you better at Wordle, which you can continue to play for its social aspects.  All of the examples in this post are from the WordMaster site.

Using this site, I’ve played many games and come up with some strategies that seem to help me solve the puzzle within six guesses at least 99 times out of 100.  Below are the main strategies I’ve discovered.

Opening Guesses

I always start off with the same two words, AILED and ROUTS.  This covers all of the vowels (except Y) and some popular consonants.  Using standard opening guesses like this may make the beginning of the game less interesting or exciting, but it produces more consistent results. Obviously there are many other words you could choose as your opening guesses, if you prefer to find out different information or just prefer different words.

The main downside of using two standard guesses to open is that your average number of guesses may go up.  With this technique, it’s less likely you’ll get lucky and solve the puzzle in three guesses or fewer.  I don’t personally care about this; I just want to solve the puzzle within six guesses virtually all the time.  Once in a while I’ll skip the second standard guess if the first one turned up, say, four hits.

Making the Most of Your Guesses

If you share my goal of solving the puzzle successfully (as opposed to getting it in fewer guesses) then you can get a different perspective on why you make the guesses you make.  Assuming you don’t play in hard mode (which seems impossible and not that much fun), you don’t need to use all of the information you already know in your subsequent guesses.  

The main purpose of each guess should be to maximize the amount of new information you get from the guess.  This often means choosing completely different letters from those that have already been revealed to be in the solution.  Of course these known letters will come back into play in your final guesses, but intermediate guesses should be fact-finding missions for what you don’t yet know.

As an example, suppose this was the result from your opening guesses:

You might think “Oh, that A probably goes in the second position” and be tempted to guess something like “games”.  Maybe you’ll get lucky, but probably not in this case.  If you think about it, there are a tremendous number of other words that also fit the same pattern.  For example: wanes, panes, manes, vanes, banes, bakes, makes, names, manes, wakes, cages, pages, wages, mages, sages, sakes, napes, vapes, paces, capes, caves, naves, paves, waves, mazes, etc.  Obviously, you don’t have enough guesses to try all of these.  If you get a thrill out of taking a big risk and trying to use your “intuition” in cases like these, then go ahead and take your best shot.  But there is a better way to solve puzzles like these.

The way to solve more reliably in cases where there are too many possibilities is to make guesses that identify which of the letters are involved first.  This will require ignoring what you already know, because guessing A in the 2nd place is probably a waste of time and guessing E and S at the end is definitely useless for giving you new information.  Instead, pick a word that covers as many of the possible letters for positions 1 and 3 as possible.  But importantly, you first just want to identify the letters, not their positions, which we already know are 1 or 3.  Looking at the list above, you can see that we’re talking about C, M, N, P ,W, K, V, G, S, and Z.  A lot of letters!  You’re doing well if you can find any legal word that has three of these consonants.  Four is ideal, but tough to do.  When I played this game, my third guess was CHAMP.

The H wasn’t really likely, but this was the best guess I could come up with, covering C, M, and P.  Note that using A in this guess wasn’t necessary, but does help provide confirmation of our expectation that A is in position 2.  We now know this with 100% certainty because positions 4 and 5 are taken and A has been ruled out of positions 1 and 3.

I hit paydirt with M, but that still didn’t narrow it down enough.  It could still be manes, makes, names, manes, mages, mazes, and maybe more I hadn’t thought of.  Still too early to be making final guesses.  I did another fishing expedition.  It was tough to come up with another guess that covered the other remaining consonants (N, W, K, V, G, S, and Z).  The best I could do was to cover K and N.  

Note that I used vowels that I already knew weren’t in the solution because all I was after was the identity of the remaining consonant.  I got lucky and found that it was K.  This made the solution 100% known:

Maybe you’re not impressed with a five guess win, but this one could have easily made you run out of guesses if you had tried to make final guesses starting on guess three.  Many of the puzzles are like this.

Keeping Notes

I’ve found it can be helpful to use the game as a way to “take notes” about what you’re thinking.  For example, suppose you got the puzzle below.  I had three letters known from my opening guesses, so I made a “final” guess on guess number 3.  Okay, DINKS is a weird word and probably not the solution, but I thought D was probably in position 1 and just made the guess.  

 

Clearly, D is in position 4, so it’s just a matter of making guesses to determine the letter in position 1, right?  But before doing that, it’s good to take a moment to figure out how many possibilities there are and if you have enough guesses left to guess the possibilities one at a time.  

This is where using the game to take notes comes in.  You can enter each possibility for position 1, as follows:

Obviously, this isn’t going to form a valid guess.  It’s just keeping track of which possibilities there are and how many possibilities exist.  I came up with four (FINDS, MINDS, BINDS, and WINDS), and I entered the starting letter for each of these possibilities.  Since there were (at least) four, this told me I didn’t have enough guesses left to guess them one at a time and be sure of solving the puzzle within six guesses.  Time to go consonant fishing again.

Taking notes like this on a consonant possibility also helps you come up with a guess that covers as many of the possibilities as you can.  After staring at FMBW for a while, I came up with WOMBS, which covered three of the possibilities.  It hit on W, after which the solution was 100% known.

When You Get Stuck

Sometimes you are confused by a puzzle and can’t come up with even a single word that fits with the known information.  You can always guess something like CHAMP or PINKY that just covers a lot of letters, but this is a last resort.  What can help you think about more likely possibilities?

This is another way I use the game board to help me think.  I come up with things I’d like to know, or possibilities I’d like to try out, and I enter these on the board with X standing in for unknown letters.  

For example, with this puzzle, I had three of the letters, but no positional information known even after three guesses.  I decided to try seeing if E could be in position 5, so I entered the pattern below to stimulate thinking along these lines:

After a while, it became clear that this wasn’t a likely pattern.  Where did the R go?  Obviously a vowel was needed in the middle of the word, but E had already been ruled out in position 3.  Was there an E in position 2, or was Y used as a vowel?  I couldn’t think of a single way this pattern could work, so I tried a different one.

This pattern included all three known letters in positions where they hadn’t already been ruled out.  So if I could come up with even one word that fit this pattern, I would likely get the positional information I needed.  I did find one word that fit the pattern, and this turned out to be the solution.  It was much easier to come up with this somewhat unusual word by staring at the template pattern with the Xs.  

Things To Remember

It’s easy for me to forget that the solution may have repeated letters.  It seems like a waste to guess a second copy of a letter when you already know it’s in the puzzle.  But repeated letters are a real possibility, so it’s important to include possibilities with repeated letters when you’re coming up with lists of possible solutions.

I also struggle to decide when to guess Y.  It’s rarely used as a vowel in the middle of the word, but sometimes is.   When it’s used at the end of a word, it can be preceded by a lot of things like L, N, D, or repeated letters like PP, TT or NN.  When I do guess it, it’s usually in position 5.

The main time I guess Y is when there doesn’t seem to be enough vowels.  However, when there’s not enough vowels, it’s more likely that a repeated copy of a known vowel is part of the solution rather than Y.  I guess Y only after repeated vowels have been ruled out.  

The other thing I need to remember sometimes is to double check my guesses and make sure that I’m not guessing something I already know to be false.  It’s a good practice to scan up the columns before entering your guess.  Look to see if the letter you’re guessing has already been guessed in that column.  Sometimes you’re forced to make a guess you know is false, but it’s a waste of a guess to do it by accident.

Summary

To summarize, I’ll just give you one more example which combines the techniques described above and shows why you should focus on gaining new information rather than guessing the solution prematurely.  

Suppose you got the following information from your opening guesses:

Now playing A again in position 1 would give you zero new information.  We need positional information on R and E, and we need information on what other letters are part of the solution.  

Here’s what I guessed:

Why is this a good guess?  We know it’s not a possible solution, since it doesn’t include A in position 1.  E in position 5 doesn’t seem likely either, since we’d need a vowel in position 2, or more likely 3, and it looks like we have all of our vowels already.   

Note, however, that this result tells us exactly where E goes with 100% certainty.  It must be in position 3 because 1 and 2 are occupied and 4 and 5 have been ruled out.  

In the meantime, this guess allowed us to try out two new consonants and gave us the position of R.

What was the answer though?  I entered the known information about A, R, and E to see if any words would jump out at me.  

Words that start with vowels are difficult for me.  I couldn’t think of any candidate solutions at first, until I remembered to consider possible repeated letters.  Then the solution came to me.  

I hope these tips help you be more successful at solving Wordle and related puzzles and that you feel smart as a result.  I still play Wordle and have fun with it.  

Fare Thee Well, Lizzy

Lizzy had a tough act to follow.  My previous cat, Sophie, was a real love bug who followed me around everywhere I went.  This was huge for me when I was living alone, so I didn't wait long to get a replacement cat when Sophie died.

I wanted to get a cat who was a few years old, in need of a home and more sedate than a younger cat.  Lizzy fit the bill, and won my heart with her cute face and super soft calico fur.  I took her home from the MSPCA at Nevins Farm in Methuen, MA to my little house in Lawrence.

Liz was not initially a people cat like Sophie was, and I'd be lying if I said I wasn't a bit disappointed.  But she wasn't mean, and would let me pet her if I sought her ought.  She just didn't need me the way Sophie had.  But we got along, and she warmed to me slowly, oh so slowly.

A few years later, Lizzy's world got turned upside down when Carol moved in with me and brought along her two cats, Sirin and little Loki.  The people at the MSPCA had not known much about Lizzy's past, so they didn't know if she would get along with other cats.  I would not say she got along well with them, but at least she didn't fight.  Loki's energy and propensity for chasing his older sister was decidedly unwelcome for Lizzy, but it did keep her on her toes.  Carol brought a lot of stuff with her too, so Lizzy became expert at finding defensible hiding places.

Things got even crazier when big, swaggering Comet joined us.  But he paid little attention to Lizzy (or the boys for that matter), so this didn't make Lizzty's life any more difficult.  It was just getting a bit crowded in our little house.

Finally, we moved to our home in the wilds of New Hampshire.  Everyone enjoyed the extra space.  Now the cats could run, and Lizzy relaxed a little since the larger house provided more places to hide from her brother.  She also proved to be by far the best mouser of the bunch.  With the patience of a Sphinx, she could outwait any hiding rodent until they came out so she could pounce.

Over the years in New Hampshire, Lizzy softened and grew closer to her family.  Sometimes even she and Loki would end up snuggling together on the bed.   My patient affection for Lizzy on her own terms was eventually repaid as she became more fond of me.  She kept me company for my morning bath (I'm sure the space heater had nothing to do with this, see above).  She even developed a habit of greeting me cheerfully when I got home from work, signalling her approval with a vigorous scratch on the scratching pad and making her head available for petting.

Luckily for Lizzy, the end came quickly.  She had only about two weeks of declining energy before fluid on the lungs signaled the beginning of real discomfort and a grim prognosis.  Benefiting from being a feline rather than a human, we helped her towards her eventual end, rather than forcing her to suffer the drawn out torment of futile treatment.

Lizzy will be sorely missed by our whole family.  With Comet gone too, it's just the two boys representing the felines.  I'll miss the satisfied face Lizzy made when getting a scritch under her chin.  We'll miss her offers of help whenever we're preparing chicken.    I'll miss her curled up on the basket in the bathroom, sandwiched between the baseboard heater and the space heater.  Fare thee well, Lizzy.  Here's hoping you bask in eternal warmth.  Thanks for keeping me company for a while.

My Summary of General Relativity

As you may know, Einstein’s theory of relativity is actually two related theories.  I wrote about the Theory of Special Relativity here, and that’s where most of the counter-intuitive weirdness is (time dilation, length contraction, and the unification of space and time into spacetime).  In contrast, General Relativity has only one big weirdness, the assertion that the “force” of gravity is an illusion, and that what we observe is just a manifestation of the fact that our spacetime is curved.  Hopefully you’ll be able to get your head around this by the end of the essay.  The math of general relativity is pretty advanced and hairy, but luckily it’s not necessary to understand this to get the gist of the theory, so I’m going to gloss over it.  It’s also not necessary to grok the concept of “spacetime” for our purposes here, so I’m only going to refer to “space”.

General Relativity gets its name from the fact that it describes all kinds of motion, while Special Relativity only describes the special case of inertial motion, which is motion that doesn’t include acceleration.  Einstein’s great insight about acceleration and gravity is that they’re the same thing. Therefore, General Relativity (GR) is a theory about accelerated motion and gravity.  

Before we get into all that, let’s review the theory that GR replaces, Newton’s Law of Universal Gravitation, which is usually given by this equation:

However, this equation is useless on its own.  To understand how gravity acts on massive bodies, we need to add Newton’s Second Law, which can be written this way:

You may be more familiar with the simple F=ma form, but since acceleration is just the change in velocity over time, the middle term should be understandable to anyone with a passing familiarity with calculus.  (For bonus points, understand that acceleration is the second derivative of position).  The reason to emphasize this is to show that the law of motion involving forces is a differential equation, which is an equation that relates quantities and their rates of change.  Einstein’s equations will also take the form of differential equations.  

The two equations above work together to tell us what to expect from gravity.  The first one says how to combine the masses of two objects with the distance between them and the mysterious constant G to calculate the force exerted on the body of interest.  We then plug the force into the second equation to calculate how the body of interest will move under the influence of this force.  

Simple and effective, Newton’s laws reigned for hundreds of years, and were utilized to calculate everything from the paths of celestial bodies and cannonballs to the interactions of billiard balls.  However, there were anomalies that Newton’s equations couldn’t explain.  In particular, the orbit of Mercury was slightly different from what was predicted by Newton’s laws.  The orbit precessed, which means the axis of rotation moved in a regular way, and nobody could explain this.

It took Einstein ten agonizing years to work his way from the Theory of Special Relativity to the Theory of General Relativity.  Reportedly, when he used his completed equations to calculate Mercury’s orbit and the precession was perfectly predicted, he was so excited he couldn’t sleep for days.

Einstein’s equations have the same two-part structure as Newton’s, but instead of a “force” being the currency traded between the two parts, Einstein’s equations use the curvature of space.  While curved space is a mental hurdle we’ll attack shortly, this is actually more intuitive, since it’s very hard to say exactly what a gravitational “force” is, beyond vacuous definitions like “the thing that makes masses move”.  Without further ado, here are the equations:

The first equation plays the role of Newton’s first equation, but instead of an “other mass” and a distance, the equation describes the curvature of space in terms of the matter density (expressed by the T term).  As I said, I’m not going to attempt to explain the math, but the quantities with the Greek indices are special matrices called tensors that contain factors for every dimension of space.  The second equation describes how objects move in a curved space.  This is clearly a differential equation, equivalent to F = ma, which is of course a special case solution when the space is flat and the second term vanishes.  In Newton’s universe, masses create forces and these forces make other masses move.  In Einstein’s universe, masses make space curve, and curved space makes masses move on paths called geodesics, which follow this curvature unless a force compels them otherwise.

Visualizing curved spaces is actually pretty easy if you limit yourself to two dimensions.  The surface of a sphere (such as the earth) is a great example you can intuitively explore.  If you compare a flat plane to the surface of a sphere, some pretty stark differences arise immediately.  On the plane, if you walk in a straight line forever, you never come back.  On a sphere, if you walk in a straight line you arrive back where you started in a finite time.  On a plane, parallel lines never meet.  On a sphere, parallel lines do meet (think of the meridian/longitude lines on earth meeting at both poles).  

Three-dimensional curved space is harder to visualize, and we’re not going to try.  It’s enough to accept that a creature trapped on a two dimensional surface who believes it is flat will be surprised at some of the phenomena of curved 2-D space described above.  If you can tentatively accept that you are a creature trapped in a curved 3-D space that you think is flat, you can anticipate that some surprising things will be observed if that space is actually curved.  

The main counter-intuitive result of the fact that we live in a curved 3-D space is that we have mistaken concepts of what “at rest” and “accelerating” mean.  We think we’re at rest when we’re standing, sitting, or lying down on something connected to the surface of the earth.  According to Einstein, this is not a rest state, it’s an accelerated state.  According to GR, the only time you’ve not been accelerating in your life is when you’ve been freely “falling” in earth’s gravity.  Probably the longest freefall you’ve experienced is the time between stepping off the high dive and hitting the water in the pool.

How can anyone say lying in bed is acceleration?  In classic Einstein style, we use thought experiments.  Imagine you’re in a closed box that appears to be an elevator car.  If this box was placed out in space an infinite distance away from any mass, you’d float freely, with no particular tendency to go to one side or another.  If you held a ball and then released it, the ball wouldn’t move.  Now imagine some force grabs one side of the elevator car and starts pulling at it, accelerating at 9.8 m/s^2.  Immediately, you would find one of the sides of the car rushing towards you.  As you hit the side, it would immediately seem to become the “floor”, and the side the force was pulling on would seem to become the “ceiling”.   If you regained your footing, it would feel just like standing up on earth.  If you held a ball in your hand, your hand would impart an acceleration to the ball which comes from the acceleration of the floor traveling through your body.  If you let go of the ball, it would stop accelerating and inertia would cause it to travel in the same direction at a constant speed.  Since the elevator car is accelerating, it would soon catch up to the ball and the “floor” would hit it.  Unless you knew what was happening, you would interpret this as the ball “falling” “down”.  This is how acceleration and gravity are the same thing, or at least indistinguishable.  

Back to you lying in bed, the matter comprising the earth and your house and bed are constantly accelerating and pushing on you.  This explains the force you feel the bed pressing against you, just like the ball experienced the force of your hand pressing against it in the elevator car.  If an empty shaft to the center of the earth suddenly appeared under your bed, you’d no longer feel the force of anything pressing against you.  Very relaxing and comfortable!  You might think that you’d start “falling” but this is only because you have a habit of comparing your motion to things on the surface of earth.  Relative to the curved space you inhabit, you’d finally be at rest (or in inertial motion, actually, so at rest in some suitable inertial reference frame), while objects on or in the earth accelerate away from you.

That’s really all there is.  It’s taken me quite a long time to become even remotely comfortable with the explanation above.   But if you want to understand how curved space explains gravity, changing your habitual notions of “at rest” and “accelerating” is the only way.

As remarkable as the Theory of General Relativity is, many mysteries about the nature of gravity remain.  Matter following geodesics through curved space makes some sense, and allows you to keep your intuitive idea of space as a set of locations that may or may not contain matter.  But the other half of the theory, where matter causes space to curve, doesn’t really have an intuitive explanation behind it.  What is matter and what is space?  How exactly does matter cause space to curve?  It may well be that space is just another mathematical fiction like Newton’s force.  It may be that there are particles called gravitons that transmit the force of gravity, and their discovery may make curved spacetime unnecessary.  We also haven’t united General Relativity and Quantum Mechanics into a theory of Quantum Gravity, so there will doubtless be many surprises when that happens.

My Summary of Special Relativity

As you may know, Einstein’s theory of relativity is actually two related theories.  The Theory of Special Relativity, published in 1905, describes the nature of space and time for the special case of inertial reference frames (coordinate systems that aren’t accelerating relative to each other and have no gravity).  The Theory of General Relativity, published ten agonizing years later, covers the more general case of accelerating reference frames, which Einstein asserted are the same as gravity.  The math involved in general relativity is much more advanced, but special relativity is where most of the counter-intuitive weirdness comes from.  This essay covers special relativity (SR).

A reference frame is a construct we use to describe a set of locations in the universe that are rigidly connected so they move together at the same speed.  Such constructs are useful because we can draw imaginary coordinate axes on them and thereby apply all the tools of mathematics to study events that happen in the frame.  Obviously, not everything in the universe is rigidly connected to everything else, and things move at different speeds.  Therefore, we’ll need many different reference frames to accurately describe the universe.  

Imagine you’re in the back of a pickup truck driving at a constant speed down a straight road, and your friend is standing on the sidewalk as you drive by.  As you and your friend wave to each other, you are in inertial reference frames that are moving relative to each other at a constant velocity, based on the speed and direction of the truck relative to the sidewalk.  When the relative velocity is constant, we say the motion of the reference frames is inertial (since the law of inertia says objects will travel in this way if no forces act on them).

It’s been know for hundreds of years that this kind of relative motion exposed deep laws of physics.  For example, if you reached out your hand and gave a high five to your friend on the sidewalk, both of you would feel the slap with equal force.  You could say your friend on the sidewalk is at rest while you and the truck are moving, but this is an arbitrary designation.  This can only be said if you affix the coordinate axes to the sidewalk.  If you fix the coordinate axes to the truck, then it’s you who’s at rest and your friend on the sidewalk who is moving relative to the coordinate axes or reference frame.  This thought experiment points out that the notion of absolute rest and motion that Newton championed is not as useful as the notion of relative rest and motion.  After all, both truck and sidewalk are on the rotating and orbiting Earth, which is in the solar system which orbits the galaxy, etc., but none of these other motions make any difference in how the participants in these experiments perceive each other.  

This simplest form of relativity is known as “Galilean relativity”, because Galileo Galilei was the first to state it clearly.  His most famous postulate of relativity is that if you were inside a windowless cabin on a ship on a clam lake, there is no experiment you could do that would tell you if the ship was at rest (relative to the lake) or moving in a straight line at a constant speed.  As soon as the ship accelerated or turned, you could feel it immediately.  We’ll come back to that when we talk about gravity, but for inertial reference frames, inertial (constant-speed straight-line) motion can’t be detected.

With Galilean relativity, velocities add up in simple ways.  This is immediately intuitive.  Imagine you’re in the back of the pickup truck with a paintball gun, preparing to prank your friend on the sidewalk.  If the truck is going 20 mph and the paintball gun shoots at 30 mph, then if your aim is true, your friend on the sidewalk will feel as if the paintball has hit him at 50 mph, because that’s its speed relative to the sidewalk.  The velocity of the paintball from the gun is added to the velocity of the truck and gun.  

This intuitive picture seemed to work, and Newton’s laws of mechanics are based on it.  The triumph of the theory of special relativity is to recognize that this isn’t quite right; it’s only an approximation.  At low speeds, it’s a very good approximation, so how was the inaccuracy discovered?  The answer involves the speed of light.

By the end of the 19th century, the speed of light was known to be finite and had been measured to some degree of accuracy.  The physicists of the day assumed that everything, including light, obeyed the principle of Galilean relativity.  Given this assumption, light had to be moving relative to something, and they gave this something the name “luminiferous ether”.  The ether was taken to be the substance which filled and defined a “universal rest” reference frame, relative to which everything else could be measured.  

Many experiments were done to try to measure the speed of the earth relative to the ether.  The first experiment that was done well enough to be trusted by the bulk of the physics community was by Albert Michelson and Edward Morely.  The Michelson-Morley experiment used an interferometer, the same instrument used in the recent LIGO apparatus that detected gravitational waves.  An interferometer uses light sent down two perpendicular arms that reflect it back to the right angle vertex.  This is generally done with a partially reflective mirror oriented at 45 degrees to a light source.  The mirror “splits” the light so that some is reflected and goes down one arm and some is transmitted and goes down the other arm.  When these partial beams are reflected back to the mirror, the two beams are partially reflected and partially transmitted again.  This combines light from both arms of the interferometer and sends the combined signal to a detector.  See this animation on Wikipedia (just the left hand side of the diagram for now).  

The lengths of the arms can be calibrated so the light that travelled on the two arms is in anti-phase when it reaches the detector.  This means all the crests of one light wave line up exactly with the troughs of the other light wave so they completely cancel each other out and the detector sees nothing.  After such a calibration, if a subsequent change in experimental conditions causes the light to take longer to travel one arm versus the other, then the light won’t be perfectly in anti-phase anymore, and the destructive interference will be incomplete.  Then the detector sees a signal, and the amount of signal can be used to measure the difference in time taken by the light that traveled the different arms.  

Michelson and Morley expected to be able to see a difference in the time taken by the two light beams when they changed the orientation of their interferometer.  In a sense, they were searching for the ether, the reference of absolute rest.  They expected that when one arm was oriented parallel to the direction of Earth’s motion relative to the ether, the path light would have to travel on this arm would be slightly longer than the light that took the path perpendicular to the apparatus’ motion relative to the ether.  See this analysis to understand why, but it’s just basic Euclidean geometry, algebra, and the assumption of Galilean relativity.  Or just look at the right side of the Wikipedia animation to get an intuitive feel for why the travel times were expected be different, resulting in a phase shift of the light beams.

The Michelson-Morley experiment is said to be the most famous and consequential “failed” experiment of all time.  Of course “failed” is the wrong word.  The experiment produced a “negative” result, meaning it didn’t show the expected signal from the expected path length differences of the two arms of the interferometer.  This negative result was a major anomaly demanding an explanation, since it contradicted the prevailing theory of a stationary ether and Galilean relativity.  And as all good anomalies do, this one spawned a scientific revolution.

If there truly was no way to measure motion relative to a fixed ether, this had immediate logical and mathematical consequences.  It was not Einstein, but several other physicists of the late 19th century who worked out these implications.  Hendrik Lorentz got a lot of the credit, and the transformations used in special relativity still bear his name.  Einstein’s major contribution was to show that the Lorentz transformations relating the velocities of relatively moving reference frames were a consequence of only two principles, and didn’t require the existence of an ether or a frame of absolute rest.  The two principles from which SR is derived are:

1. The laws of physics have the same form in all frames of reference.
2. The speed of light is the same for all observers in all frames of reference.

The first principle is an axiom, taken as given without proof.  Most people don’t have a lot of trouble accepting it, but the second principle is a bit more counter-intuitive.  It basically says that Galilean relativity is false.  It doesn’t have to be taken on faith, since that’s what you get if you believe the results of the Michelson-Morley experiment are correct.  They observed that light travelled the same speed no matter how they oriented their apparatus relative to the orbital motion of the earth.  People didn't notice the departure from Galilean relativity until the late 19th century because it only becomes significant for things traveling near the speed of light.  The value of the speed of light, c (approximately 3 x 10^8 m/s or 186,000 mi/s), also falls out of Maxwell’s Equations of electromagnetism, which led Maxwell to propose that light was an electromagnetic wave.

The Lorentz transformation is simply a set of formulas that allow you to convert distances and time in one reference frame to these same quantities with respect to another reference frame that’s moving inertially relative to the first.  When making up such formulas, it’s convenient to pick our coordinate systems so that the relative motion only occurs in the x-axis direction.  In that case, Galilean relativity has a simple transformation:

where x, y, and z are the coordinates in the “first” reference frame (which we’re choosing to call “at rest”), the primed coordinates are the “moving” reference frame, and v is the relative speed of the reference frames.  This is the transformation used in the example above to determine that the speed of the pickup truck and the paintball should be added together to determine what speed your friend on the sidewalk perceives (the minus sign could be a plus sign, depending on how you choose your coordinates).  

The Lorentz transformation is a little more complicated:

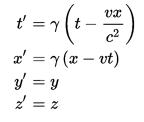 where

The gamma factor is simpler than it looks.  If your speed is much less than c (the speed of light), then the second term under the radical (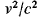) is very close to zero.  When that happens, gamma is very close to 1, and the Lorentz transformation approximately reduces to the Galilean transformation.  (This is why Galilean relativity seemed right for so long).  On the other hand, if your speed is very close to c, then the value of gamma skyrockets.  Here are some sample values:

The most surprising thing about the Lorentz transformation is that the x coordinate isn’t the only one affected by relative motion in the x direction.  The time coordinate is also affected.  This makes a little more sense when you realize the whole purpose of creating the transformation in the first place was to make the speed of light constant in all reference frames.  Since speed is distance/time, of course time must be affected in order to keep the distance/time ratio constant.

This mixing of space and time is what gives SR some of its truly weird and counterintuitive properties.  I don’t know if people can get used to it, but I haven’t yet.  If you plot the x and t coordinates (omitting y and z since they’re not interesting and we run out of dimensions to draw them in) along with the primed x and t coordinates, we get this remarkable plot:

Notice how the primed axes no longer appear to be at right angles to each other.  However, this is only because we’ve drawn the graph from the perspective of the unprimed coordinates.  Unexpectedly, if we adopted the other perspective, the primed axes would look “normal” and the unprimed axes would appear in exactly the same positions as the primed axes shown above.  This illustrates the counterintuitive reciprocal nature of the time and length dilation effects.  

For any “event” that occurs on this “spacetime” graph, the two different coordinate systems will ascribe different relative amounts of space vs. time to the event.  The rectangle and parallelogram on the diagram are meant to represent “dropping a perpendicular” to each coordinate axis in order to measure an event’s position and time.  Notice the different amounts of time and space ascribed by the two coordinate systems to the event at the upper right corner of the rectangle and parallelogram (compared to another imagined event at the shared origin).

The only things that are unchanged in both coordinate systems are the 45 degree x = t and x = -t lines.  These represent light rays travelling in the positive and negative x directions.  (The units have been chosen so that the speed of light is equal to 1).  Again, this shouldn’t be surprising since the whole purpose of all of this is to construct an analytic framework where the speed of light is constant in all inertial reference frames.  

Newtonian physics and Galilean relativity don’t rotate space and time into each other like this.  Newton never had the need to add a time axis to his motion diagrams because he assumed there was one absolute reference of time, and that it was possible to consider “all points in space at a given time”.  This is simply not possible when it’s a different time at different points in space that are moving relative to one another.  In SR, clock readings can only be made locally.  We normally make assumptions about what distant clocks read, but these assumptions are invalid.  As long as you insist on thinking of space and time separately, as if there existed “all of space at a given time” then SR will seem bizarre and paradoxical.  Well, there is no unique time for all of space.  Doesn’t exist.  You were misinformed.  Get over it.

The easiest way to start to accept that there is no absolute universal time is to understand the relativity of simultaneity.  That is, whether or not two events are simultaneous depends on how you’re moving relative to the events.  All other times reduce to this, since you’re always comparing one event of interest to another event (the tick of a clock).    If you believe the tilted coordinate axes described above, then this animation from Wikipedia should convince you that events can be simultaneous in one reference frame, non-simultaneous in another, and non-simultaneous in the opposite order in yet a third reference frame (the white bar represents the progression of time in the reference frames).  If you aren’t on board with the tilted axes, then try this video.  

How can events occur in different orders depending on who’s watching?  Doesn’t that potentially mix up the order of cause and effect?  No, because the order of events can only change for events with spacelike separation.   To understand what this means, you need to imagine that every event has a “light cone” that precedes and follows it.  The surface of the cone represents the possible paths light rays can take.  As shown below, this is a spacetime diagram where units are again chosen so the speed of light is 1 (it plots at 45 degrees), the vertical axis is time, and only two spatial dimensions are shown.

 

If one event is caused by another, then the effect event must be inside the light cone of the cause event, since some some signal or piece of matter must pass between them for them to be causally related, and nothing can travel faster than the speed of light.  Events with spacelike separation do not have light cones that overlap, so they are said to be causally disconnected.  For causally connected events, all observers will agree on the order of events, so causality is saved.  The diagram below shows several light cones that can be imagined to represent causally connected and causally disconnected events.  Only a timelike path can connect causally related events.

The ultimate effect of the Lorentz transformation is that relatively moving observers disagree about both time and distance.  This leads to the fact that moving observers experience both time dilation and length contraction.  Time dilation as derived from the Lorentz transformation is expressed with this formula relating the difference in time (𝝙t) between two events in primed and unprimed coordinate systems:

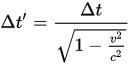
In this formula, the closer v gets to c, the smaller the quantity under the radical becomes, and the larger the primed 𝝙t becomes compared to the unprimed 𝝙t.  This means if you’re moving relative to a clock, the clock will appear to be running slowly, since your 𝝙t is larger than the 𝝙t in the clock’s reference frame.  However, in the clock’s reference frame, it appears to be running normally.   This result has been verified by flying atomic clocks around on planes and then later comparing them to ground-based clocks.  Taking this to the extreme, if you could actually travel at the speed of light, a clock at rest would appear to be standing still.  

The Lorentz transformation can be used to derive the following formula for length contraction of an object as seen from a reference frame moving relative to that object:

where L0 is the length of the object in the reference frame where it is at rest, v is the relative speed of the two reference frames, and 𝛾(v) is shown in expanded form on the right.  This formula shows that if the relative motion is much slower than the speed of light, the length is nearly the same in both reference frames.  As the relative speed approaches c, the length of the object as seen from the moving reference frame approaches zero.

Is there anything that stays the same in every inertial reference frame?  As a matter of fact, there is.  If you combine the space and time separation (deltas) between two events using the formula below, you get the quantity on the left hand side, which is called the “spacetime interval”:

The wonderful thing about the spacetime interval is that it’s invariant, meaning it won’t change when you view the two events from a different reference frame that’s moving inertially with respect to the first.  The two reference frames may see different amounts of space vs. time, but the spacetime interval will always be the same.

An even more remarkable takeaway from this formula is that c is essentially used as a conversion factor between time and space.  The remarkable thing is not that electromagnetic radiation is observed to move at this speed, but that such a fixed conversion factor exists at all.  

This conversion factor between time and space also leads to the last thing I’ll say in this essay on special relativity.  The fact is, everything, including you, is always travelling through spacetime at the speed of light.  If you are sitting still in your reference frame, then all of your spacetime travel is along your time axis, and you’re travelling on that axis at the speed of light, as the spacetime interval formula indicates.  As soon as you start travelling in space, then some of your velocity is used up by this travel, and your progress through time must be less than c (as seen from your former rest frame).  This is one way to look at time dilation (your clock will be seen as running slow by an observer you left behind).

What does this say about light itself?  The time dilation formula:

isn’t very helpful.  If you imagine a photon that left a distant star a billion years ago and entered your eye just now, then in your unprimed coordinates, 𝝙t is one billion years.  The reference frame of the photon is moving at c, so the denominator in the formula is zero.  This prevents us from calculating 𝝙t'.  No matter what 𝝙t is (no matter how far away the star is), the result is the same.

This says that light is expending all of its velocity on travel through space, so there’s no velocity left for travel through time.  This seems to indicate that time does not pass at all for a photon.  You could try to say that 𝝙t' for the photon is infinity, or zero, but neither one really works.  There is an incredible variety of answers to this question on the Internet, and most of them are pretty incoherent.  If you ever get a chance to talk to a photon and ask it what happened on its trip, please let me know.