Saturday, February 27, 2016
9/11 - Negotiation = Trump
When I was growing up in the 60's and 70's, airport security was nonexistent by today's standards, and planes getting hijacked was a thing that happened from time to time, like school shootings today. In those days, some of the hijackings were political, but many were just done for money. Commandeering a plane was just a way to acquire a bunch of hostages whose lives could be traded for cash. This rarely worked out for the hijackers, whose plane would often be taken away from them by force, even if innocent lives were inevitably lost along the way.
These hijack-for-profit extortionists would kill hostages if necessary to gain tactical advantage, but murder didn't seem to be their primary goal. So I thought the authorities should just pay the ransom to ensure the safe release of all the innocents. It had to be explained to me why this seemingly obvious strategy was a naive idea. The way it went was that if we give in to their demands, this will only encourage other groups to copy the same strategy, resulting in even more hijackings in the future.
Even this meager reasoning has been lost in today's rhetoric on terrorism. Leaders from all countries and of all political persuasions just flatly state: "we don't negotiate with terrorists". Why is this policy never examined? In the hostages-for-cash scenario, there is a certain grim logic to the reasoning, but does the same calculus necessarily apply to today's political terrorism?
You might think the same logic applies universally, but a deeper analysis shows otherwise. True, if political groups got what they wanted, their tactics might become more popular in the future. But what do they want? Would the demands of all similar groups be insatiable, growing without bound until the whole world was engulfed in perpetual terror?
If you only consume mainstream news, you wouldn't even know they had any demands, let alone what they are. Terrorist groups like Al Qaeda, ISIS and the like are depicted as mindless sub-humans, bent on a completely irrational path of destroying us Westerners, who are just minding our own business when they strike out at us. Within this narrative, the only acceptable response is to annihilate them with superior violence.
This characterization of today's terrorists is false. They are human beings, trying to build a society just like us. They have very specific demands of us, many of which are quite reasonable. Meeting their demands would inevitably involve a reduction in western violence in their lands, which would cool the anger that's directed back at us. Therefore, negotiation and willingness to meet some of their demands would result in a de-esalation of violence.
How did I come by such a contrary viewpoint? Is it hopelessly naive? A turning point for me was reading the book Imperial Hubris. Unless you read a source like this, you and I can't have a rational discussion about things, because you're wallowing in ignorance. Did you know that Al Qaeda articulated a very short, very specific list of demands, years before 9/11? Why was this not widely reported, especially after 9/11 resulted from our failure to meet their demands? Because the unconditional, unexamined "we don't negotiate with terrorists" mantra makes such thoughts unthinkable, let alone admissible in public debate.
If we at least entertain the possibility that people acting with violence are rational human beings who are simply out of options, then ending the cycle of violence becomes possible. Why is this unthinkable? The United States acts with violence, yet most Americans consider this rational, just and necessary action. Why isn't the "enemy" given the same benefit of the doubt? Answer: because they've been dehumanized so we don't need to consider their concerns.
What are the demands Al Qaeda made prior to 9/11? Things like 1) Stop militarily occupying Muslim holy lands, 2) Stop propping up corrupt dictators in the Arab world, and 3) Stop blind support of Israel and dehumanization of the Palestinians. Are such demands really beyond the pale, not even worthy of discussion? To the US political and media elite, they apparently are, but what do you think? Read Imperial Hubris and decide for yourself how bad the bad guys really are.
How does Donald Trump fit into this story? I'll argue that someone like him is inevitable when a refusal to negotiate with others is the universal stance on both sides of the political divide in America. Through eight years of Bush and eight years of Obama, the narrative pushed by both parties and their allied media has been the dehumanization of Muslim enemies, and a refusal to even admit they could have legitimate grievances with us. When was the last time you saw a media interview of someone from a group branded as terrorist by the US? Obama can talk about how we're at war with the Terrorists(TM), not Islam, but this doesn't help. If Obama is such a nuanced, thoughtful statesman, why can't he admit the terrorists themselves are also human beings?
When superior violence is the only acceptable response to terrorism, escalation is inevitable, as the history of the War on Terror has shown. If a genuinely peace-minded leader emerged and tried to negotiate with terrorists, the media would crucify him. Opponents would call him a terrorist-lover, and the media would repeat this without challenge. Authoritarianism through superior violence saturates our culture, from school to policing to war. In such an atmosphere, one begins to wonder why it took so long for a Trump to appear. And the media look around in horror, wondering how this could have happened, never considering their role in making it inevitable.
Did you know that Al Qaeda's threat, if their demands weren't met, was to draw us into an endless, global war that would bankrupt us? That gives you a different take on 9/11 and the War on Terror, doesn't it?
How can we get out of this mess? Start making negotiation a regular part of foreign policy discussions. Remember when diplomacy used to be a respected role? Today, diplomats only role is to convey threats of violence in euphemistic language. The media can change this by simply asking questions. Why has the so-called terrorist group done this horrifying act? What do they hope to gain? Why do they hate us? Are their demands reasonable or not? These questions have answers, but we never hear them because journalists and public officials never ask. You can start by asking them yourself.
Saturday, January 2, 2016
My Summary of Quantum Mechanics
As some of you know, I have an interest in physics. I’ve been reading “popular” books for many years, marveling at the strangeness of our universe. Eventually I became frustrated with popular accounts, where authors interpret the math and experimental results for us. It seemed to me that many authors were in love with complexity and paradox. They said the math was just that way, indeed the universe was just that way. I doubt the universe is fundamentally paradoxical, and I decided I could no longer take their word for it. I decided to learn physics for real, with the math.
As an electrical engineering major, I took a full series of calculus and a couple of physics courses. I thought I could rely on this background and just jump into a mathematical treatment of quantum mechanics, which seemed the richest source of paradox. I shortly had to admit that after 30 years, calculus can be utterly and completely forgotten. Plus, I had never completed linear algebra. Undaunted, I started a thorough math review that included calculus, some pre-calc concepts, and linear algebra. This was done mostly on Coursera and Khan Academy.
After this prep, I still could not penetrate the two QM books I had in my possession, and I became depressed. Then it occurred to me to ask the Internet if there was a better book. The Internet delivered, in the form of a recommendation for David J. Griffiths’ book Introduction to Quantum Mechanics. This book made all the difference for me. It’s crystal clear, and builds up the concepts in a logical way that other books don’t for some reason. He even includes an appendix that teaches you the specialized linear algebra concepts you need to know. I read the first three chapters quite closely, but mostly skipped the problems and skimmed many of the later chapters that went over complex calculations that didn’t interest me.
So, what does the theory of Quantum Mechanics tell us? What does the math look like? Other books had given me the impression that QM was based on linear algebra, but this isn’t really true. It’s based firmly on calculus, like other parts of physics. In this respect, I think it’s misleading to say that QM is somehow “discrete”. It’s true that things like the energy levels in atoms are calculated as a set of discrete values, and yes, linear algebra is used in these calculations, but these solutions come ultimately from equations of good old fashioned continuous variables. This is especially true of Schrodinger’s Wave Mechanics formulation, but seems equally true in Heisenberg’s Matrix Mechanics formulation, where matrix elements are computed as Fourier coefficients of functions of continuous variables.
The foundation of quantum (wave) mechanics is the wave function, denoted by the Greek letter psi. The wave function is a function of four continuous variables (time and three spatial variables), and represents the state of the system being examined. Thus, each system has a different wave function, just as each system has a different equation of motion in classical mechanics. In both schemes, the time evolution of the system’s state function is governed by a differential equation. In classical mechanics, it’s Newton’s laws, i.e., F = ma (which is a differential equation since a is the second derivative of position). In QM, the time evolution of the system’s state is governed by the Schrodinger Equation. This differential equation is complicated enough if you pretend space has only one dimension (x), so that’s how it’s normally introduced.
Here i is the imaginary unit, h is Plank's constant, m is the (non-relativistic) mass of the system (i.e., particle), Psi is the wave function, V is the potential affecting the particle, and H is the Hamiltonian. a representation of the total energy of the system.
A “solution” of a differential equation is any function that varies in the required way that the differential equation is satisfied. Now, partial differential equations are notoriously hard to find solutions for, and the time-dependent Schrodinger equation above contains differentials of Psi with respect to both position and time. So as a practical matter, the equation is separated into a time-dependent part and position-dependent part. This results in a simpler equation called the time-independent Schrodinger Equation, whose solutions are the so-called “stationary states” (because they don’t evolve in time).
It turns out that the solutions to the general (time-dependent) Schrodinger Equation can always be expressed as linear combinations of the stationary states. It’s these linear combinations that account for one of the oft-cited mysterious features of QM, superposition. When the state of the system is a combination of sub-states, people say that the sub-states are superposed, i.e., simultaneously true to some fractional degree.
When a system’s state is measured, only one of the sub-states is found, but more on this later. In this way, measurements become one of the other mysterious features of QM. What people say is that the system’s state (i.e, wave function) was in a superposition (e.g, linear combination of sub-states) before measurement, and that the act of measurement “collapses” the wave function to only one of the sub-states. Mathematically, this happens because the result of a measurement is calculated by multiplying a particular matrix by a vector representation of the state, Psi. So in this case, the elements of the vector are actually functions (the stationary state solutions to the time-independent Schrodinger Equation). So this is where the linear algebra comes in, but the vector space is an infinite-dimensional space of orthogonal wave functions . The functions and matrices are rather special, so it always turns out that the wave functions are eigenvectors of the measurement matrix. An eigenvector of a matrix is a vector that comes out merely scaled (rather than, say, rotated or otherwise distorted) when multiplied by the matrix. The scaling factor is called the eigenvalue, and in general is different for each eigenvector and matrix. Each type of measurement, e.g., position, momentum, or energy, is represented by a different matrix, usually called an operator.
That’s the gist of it. Doing physics involves defining a system with some initial conditions, solving the Schrodinger Equation, and then computing the different eigenvalues that may be returned by a measurement. However, the theory cannot say which eigenfunction/eigenvalue pair may be selected by a given measurement. It could be any of the component wave functions in the system’s superposed state. The theory can say only the probability of selecting a certain component out of the superposition, which equals the square of the coefficient each component has in relation to the other components in the superposition. For this statistical interpretation to make sense, the wave function must satisfy the property that the sum of all probabilities is 1, i.e.,
This requirement not only means that all acceptable wave functions must be “square integrable”, but also that they typically must be “normalized”, which means multiplying then by some factor that makes the integral above equal 1, rather than whatever it equaled when you chose the wave function. This strikes me as a massive hack, albeit a hack that works. Wave functions are guessed and normalized (i.e., fudged) so that they fit into the statistical interpretation of measurements of the wave function state. The normalization requirement also rests on the assumption that the probabilities sum to 1 because “the particle must be found somewhere”, (or found with some energy, if that’s what’s being measured). All of this is not derived from some physical principle or logical necessity. It’s all just cobbled together into a system that happens to be useful for measuring the things we know how to measure.
This statistical interpretation of the measurement operation is perhaps the most frustrating part of QM for me and many others. It certainly seems to be the jumping off point for how to interpret the theory, which is my main interest. What struck me in my study is how ad-hoc the whole scheme is, and how far divorced from physical reality the math is. In classical mechanics, a particle “really has” the properties represented by the quantities in the equations, and if you make a measurement, you get the instantaneous value of one of the variables. I believe, along with Einstein, that a proper atomic theory should be the same way.
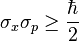
That’s standard deviations, as in the statistical properties of repeated measurements. Thus, the principle says nothing about the “actual” properties of a single particle, but only about the statistical character of repeated experiments done on multiple particles that start in the same state.
The statistical interpretation of QM is also the source of the famous “uncertainty principle”. Many authors speak, wrongly, as if the uncertainty principle applies to a single particle, saying that the more precisely a particle’s position is known, the less precisely its momentum can be known. (There are other pairs of complementary properties also). This is not at all what the uncertainty principle says. Being part of the statistical interpretation, the uncertainty principle states that the product of the standard deviations of two complementary observables has a lower limit:
That’s standard deviations, as in the statistical properties of repeated measurements. Thus, the principle says nothing about the “actual” properties of a single particle, but only about the statistical character of repeated experiments done on multiple particles that start in the same state.
Now it isn’t quite fair to compare quantum measurements with classical measurements. For classical measurements, you can generally devise a measurement apparatus that doesn’t significantly disrupt the phenomenon being measured. Not so for quantum phenomena at the atomic level. You can’t just “look at” an electron to see where it is. Shining even a single photon onto the electron will invariably alter the electron’s state in a large way. But this is the only way we know how to do measurements.
I believe the limitation of statistical predictions is a shortcoming of QM theory and our disruptive experimental techniques. It’s hard to imagine other experimental techniques, but I believe there is some underlying reality that’s described deterministically by a theory beyond quantum mechanics. Many others follow Bohr in insisting that the theory is complete and that our universe “really is” statistical in nature, composed of superpositions, etc. I don’t see any basis for such an interpretation. In my view, QM is simply a limited calculation tool. People make all sorts of assumptions about how particles exist in certain states and how wave functions collapse, when in fact these are just assumptions, not facts. Many equations and experimental results are wildly over-interpreted beyond what they actually reveal. We have no idea yet what “really exists” at the atomic level. We have some operational theories that give good predictions for some experiments, but I don’t think we can say what nature really “is”.
My future studies of QM will delve into what exactly is a “measurement”. How does the apparatus work? Why are they so destructive? Some people believe that the wave function collapse is not a real phenomena, but simply an apparent one that is a result of the system under study becoming entangled with the measurement apparatus so that the system’s wave function experiences “decoherence”. When I find out what that means, I’ll let you know,
Subscribe to:
Comments (Atom)